Chapter 12  Case study: Ant trails

Chloe Vilain and Andrew Pikler

12.1  Introduction

In nature, ants scavenge for food as a swarm. They choose their paths from the nest based on pheromone density, favoring paths with higher concentrations of pheromone. Individuals lay pheromone trails upon finding food, allowing other members of their colony to passively follow them to the food source. Because paths leading to food have higher pheromone density, increasing numbers of ants choose these successful paths. As a result, ant trails transition over time from random paths to streamlined routes. This organization and appearance of patterns over time is an example of emergence, the process by which complex systems and patterns arise from a multiplicity of simple systems.

Ant feeding patterns lend themselves to simulation with agent-based models, which simulate the actions and interactions of autonomous agents to assess their effects on the system as a whole. When we model ant feeding patterns, each ant is an agent in the model, a self-governing individual that makes decisions based on its surroundings. When simulating large numbers of ants, behavior emerges that is reflective of ant behavior in the natural world. Beyond being intrinsically fascinating, such models have applications in the “real world” in areas ranging from city planning to film production.

12.2  Model Overview

We can see one example of an agent-based model in Deneuborg et al.’s 1989 paper The Blind Leading the Blind: Modeling Chemically Mediated Army Ant Raid Patterns, available from http://www.ulb.ac.be/sciences/use/publications/JLD/58.eps.

The premise of the model is that as ants move around they deposit a pheromone, which increases the likelihood that other ants will follow the same path. Ants that have found food lay more pheromone than ants that haven’t, making it likely that other ants will follow their paths to find more food.

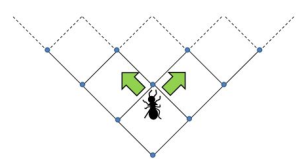
The ants live in a two-dimensional world of discrete points arranged in a grid. At each step of the model, each ant has a certain probability of moving to one of two neighboring coordinates in the direction the ant is facing, away from the nest—forward left or forward right (see Figure 12.1). All ants start in a corner of the world, which we call the nest; at each time step of the simulation, we add more ants to the nest. This leads to a constant stream of outgoing ants.

---

Figure 12.1: At each time step, ants move forward left or forward right.

---

Once an ant has found food, it turns back towards the nest. It obeys the same rules for motion—that is, in each time step, its choice to move either forward left or forward right is influenced by the amounts of pheromone it sees, except now, these choices take it back towards the nest. Also, after moving, the ant lays more pheromone than it did while foraging for food. This significantly increases the probability that other foraging ants will follow its path to find, potentially, more food.

---

Figure 12.2: The simulation after 1000 time steps.

---

In its starting configuration, each point in the world has a chance of containing food. Once this starting condition has been set, we let the simulation run for about 1000 time steps, and plot the result. You can see the plot of one such simulation in Figure 12.2, which is similar to the actual foraging patterns Deneuborg et al. present in their Figure 1.

12.3  API design

Challenges of writing a simulation such as this include designing classes that are easy for human readers of the code to understand, and implementing data structures that allow the code to execute efficiently.

One way to break up a model into classes is to list the main nouns you use when describing the model, and then represent the most prominent of those nouns as objects. In our model, the primary objects are the World, which contains Ants, and Locations that represent points in the grid.

The next step is to decide what information about the current state of the model an instance of each class is responsible for. In our case, the behavior of the World is defined by what Ants and Locations can do, so it makes sense to design our classes bottom-up and consider the World only once we have at least a tentative idea for the methods and attributes of Ants and Locations.

For Ants, the most important information is where they are in the World, so each ant has the attributes x and y to store its coordinates. Also, each Ant keeps track of whether or not it is currently carrying food. Each Ant has only local information about the World; keeping track of all the Ants is the job of the World object itself.

Ants provide two methods the World uses to interact with them:

• getPos: Returns the current coordinates of this Ant.
• move: Collects local information and moves the Ant accordingly.

Locations know even less than Ants; each Location only keeps track of the food and pheromone it contains. Locations provide accessor methods that Ants and the World use to modify the Location’s food and pheromone amounts.

Locations do not keep track of their coordinates on the map, because they never change. Instead, this information is represented implicitly by a dictionary that maps from coordinates to Location objects.

There is only one World object; this instance keeps track of all existing Ants and Locations. The World provides methods for controlling the state of the simulation: move_ants advances the simulation by one time step by calling every existing Ant’s move method, and evaporating a proportion of pheromone from each Location. Other methods include add_ants, which adds a specified number of ants to the nest, place_food, which puts food at each Location with some probability, and get_location, which looks up the Location at given coordinates.

12.4  Sparse matrices

The group of Locations that make up our World is implemented as a sparse matrix. In this representation, Locations don’t exist until they are needed; World.get_location is responsible for fetching either the existing Location at the given coordinates, or creating a new Location if it doesn’t exist.

An alternate implementation would be a dense matrix, either a Python list of lists or a Numpy array. In our case, the sparse matrix has two advantages:

• Since most of the World is empty most of the time, it is more memory-efficient to only keep track of those Locations that aren’t empty.
• A sparse matrix doesn’t have preset boundaries, so an Ant is free to wander off in any direction. It would be more difficult to implement this feature with a dense matrix.

12.5  wx

We use the wx Python package to plot a picture of the ants after the simulation finishes running.

We define a class called AntPlot which takes a World, creates a wx window, and plots the ants (see in Figure 12.2):

class AntPlot:
    def __init__(self, world):
        self.world = world
        self.app = wx.PySimpleApp()
        self.w = 500
        self.h = 500
        self.frame = wx.Frame(None, -1, 'Ant Plot', size=(self.w, self.h))
        self.canvas = FloatCanvas(self.frame, -1)
        
    
    def draw(self):
        positions = self.world.get_ant_dict()
        for pos in positions:
            x, y = pos
            x -= self.w / 2
            y -= self.h / 2
            self.canvas.AddPoint((x, y))
        self.frame.Show()
        self.app.MainLoop()

We use a wx FloatCanvas to plot the ants. Most canvases in GUI libraries define the point (0, 0) as the upper left corner of the canvas and have x increase to the left and y increase down, but the coordinates in the FloatCanvas work like in math—the origin is the middle, and the positive y direction is up. This allows us to write simpler code because we don’t have to transform our coordinates to the canvas’s system.

If you are interested in exploring wx further, AntPlot might be a good starting point.

12.6  Applications

Agent-based models have numerous applications, from modeling traffic patterns to creating realistic battle simulations. The entertainment industry uses agent-based models to simulate crowds in films, games, and advertisements.

This kind of modeling is more scalable than filming; it is easier to simulate a large crowd than to recruit a thousands of extras. Agent-based models make it feasible to create large-scale, visually stunning sequences.

The Lord of the Rings trilogy is a salient example. Visual effects developers were tasked with creating battles with hundreds of thousands of soldiers from a variety of races with different fighting techniques. They implemented an agent-based model where each agent had about 200 possible motions (animated using motion capture). Agents followed simple rules to chose possible responses based on logic and probabilities. Different races—elves, orcs and men—were based on the same “master agent” but had different weapons, abilities and programmed attack responses.

Simulating thousands of agents in tandem allowed for exceptionally complex battle sequences. The results sometimes surprised even the programmers—in one simulation, a number of agents fled the battle. They were not programmed to flee; that is, fleeing was not explicitly an option. Rather, this behavior emerged from the interaction of agents following simple rules. This unexpected action, which would be realistic in an actual battle scenario, demonstrates the power of agent-based models.

The software developed for the trilogy, called Massive, has become the industry standard for simulating large-scale battle sequences. Massive has since been used for battle sequences in movies like Chronicles of Narnia and 300, and for more benign crowd simulations Happy Feet and Avatar.

The models used in these films are more complicated than our simulated ant trails, but they are examples of the same concept. Like the agents in Lord of the Rings, our ants follow simple rules, but their interactions yield realistic, complex, and sometimes unpredictable, behavior.

Like this book?

Are you using one of our books in a class?

Think Bayes

Think Python

Think Stats

Think Complexity