This HTML version of the book is provided as a convenience, but some math equations are not translated correctly. The PDF version is more reliable.
Chapter 7 Zero-finding
7.1 Why functions?
The previous chapter explained some of the benefits of functions, including
- Each function has its own workspace, so using functions helps avoid name collisions.
- Functions lend themselves to incremental development: you can debug the body of the function first (as a script), then encapsulate it as a function, and then generalize it by adding input variables.
- Functions allow you to divide a large problem into small pieces, work on the pieces one at a time, and then assemble a complete solution.
- Once you have a function working, you can forget about the details of how it works and concentrate on what it does. This process of abstraction is an important tool for managing the complexity of large programs.
Another reason you should consider using functions is that many of the tools provided by MATLAB require you to write functions. For example, in this chapter we will use fzero to find solutions of nonlinear equations. Later we will use ode45 to approximate solutions to differential equations.
7.2 Maps
In mathematics, a map is a correspondence between one set called the range and another set called the domain. For each element of the range, the map specifies the corresponding element of the domain.
You can think of a sequence as a map from positive integers to elements. You can think of a vector as a map from indices to elements. In these cases the maps are discrete because the elements of the range are countable.
You can also think of a function as a map from inputs to outputs, but in this case the range is continuous because the inputs can take any value, not just integers. (Strictly speaking, the set of floating-point numbers is discrete, but since floating-point numbers are meant to represent real numbers, we think of them as continuous.)
7.3 A note on notation
In this chapter I need to start talking about mathematical functions, and I am going to use a notation you might not have seen before.
If you have studied functions in a math class, you have probably seen something like
| f(x) = x2 − 2x −3 (1) |
which is supposed to mean that f is a function that maps from x to x2 − 2x −3. The problem is that f(x) is also used to mean the value of f that corresponds to a particular value of x. So I don’t like this notation. I prefer
| f : x → x2 − 2x −3 (2) |
which means “f is the function that maps from x to x2 − 2x −3.” In MATLAB, this would be expressed like this:
function res = error_func(x)
res = x^2 - 2*x -3;
end
I’ll explain soon why this function is called error_func. Now, back to our regularly-scheduled programming.
7.4 Nonlinear equations
What does it mean to “solve” an equation? That may seem like an obvious question, but I want to take a minute to think about it, starting with a simple example: let’s say that we want to know the value of a variable, x, but all we know about it is the relationship x2 = a.
If you have taken algebra, you probably know how to “solve” this equation: you take the square root of both sides and get x = ± √a. Then, with the satisfaction of a job well done, you move on to the next problem.
But what have you really done? The relationship you derived is equivalent to the relationship you started with—they contain the same information about x—so why is the second one preferable to the first?
There are two reasons. One is that the relationship is now “explicit in x;” because x is all alone on the left side, we can treat the right side as a recipe for computing x, assuming that we know the value of a.
The other reason is that the recipe is written in terms of operations we know how to perform. Assuming that we know how to compute square roots, we can compute the value of x for any value of a.
When people talk about solving an equation, what they usually mean is something like “finding an equivalent relationship that is explicit in one of the variables.” In the context of this book, that’s what I will call an analytic solution, to distinguish it from a numerical solution, which is what we are going to do next.
To demonstrate a numerical solution, consider the equation x2 − 2x = 3. You could solve this analytically, either by factoring it or by using the quadratic equation, and you would discover that there are two solutions, x=3 and x=−1. Alternatively, you could solve it numerically by rewriting it as x =± √2x+3.
This equation is not explicit, since x appears on both sides, so it is not clear that this move did any good at all. But suppose that we had some reason to expect there to be a solution near 4. We could start with x=4 as an “initial guess,” and then use the equation x = √2x+3 iteratively to compute successive approximations of the solution.1
Here’s what would happen:
>> x = 4; >> x = sqrt(2*x+3) x = 3.3166 >> x = sqrt(2*x+3) x = 3.1037 >> x = sqrt(2*x+3) x = 3.0344 >> x = sqrt(2*x+3) x = 3.0114 >> x = sqrt(2*x+3) x = 3.0038
After each iteration, x is closer to the correct answer, and after 5 iterations, the relative error is about 0.1%, which is good enough for most purposes.
Techniques that generate numerical solutions are called numerical methods. The nice thing about the method I just demonstrated is that it is simple, but it doesn’t always work as well as it did in this example, and it is not used very often in practice. We’ll see one of the more practical alternatives in a minute.
7.5 Zero-finding
A nonlinear equation like x2 − 2x = 3 is a statement of equality that is true for some values of x and false for others. A value that makes it true is a solution; any other value is a non-solution. But for any given non-solution, there is no sense of whether it is close or far from a solution, or where we might look to find one.
To address this limitation, it is useful to rewrite non-linear equations as zero-finding problems:
- The first step is to define
an “error function” that computes how far
a given value of x is from being a solution.
In this example, the error function is
f : x → x2 − 2x −3 (3) Any value of x that makes f(x) = 0 is also a solution of the original equation.
- The next step is to find values of x that make f(x) = 0. These values are called zeros of the function, or sometimes roots.
Zero-finding lends itself to numerical solution because we can use the values of f, evaluated at various values of x, to make reasonable inferences about where to look for zeros.
For example, if we can find two values x1 and x2 such that f(x1) > 0 and f(x2) < 0, then we can be certain that there is at least one zero between x1 and x2 (provided that we know that f is continuous). In this case we would say that x1 and x2 bracket a zero.
Here’s what this scenario might look like on a graph:
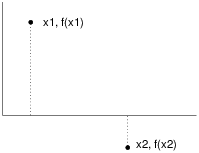
If this was all you knew about f, where would you go looking for a zero? If you said “halfway between x1 and x2,” then congratulations! You just invented a numerical method called bisection!
If you said, “I would connect the dots with a straight line and compute the zero of the line,” then congratulations! You just invented the secant method!
And if you said, “I would evaluate f at a third point, find the parabola that passes through all three points, and compute the zeros of the parabola,” then... well, you probably didn’t say that.
Finally, if you said, “I would use a built-in MATLAB function that combines the best features of several efficient and robust numerical methods,” then you are ready to go on to the next section.
7.6 fzero
fzero is a built-in MATLAB function that combines the best features of several efficient and robust numerical methods.
In order to use fzero, you have to define a MATLAB function that computes the error function you derived from the original nonlinear equation, and you have to provide an initial guess at the location of a zero.
We’ve already seen an example of an error function:
function res = error_func(x)
res = x^2 - 2*x -3;
end
You can call error_func from the Command Window, and confirm that there are zeros at 3 and -1.
>> error_func(3) ans = 0 >> error_func(-1) ans = 0
But let’s pretend that we don’t know exactly where the roots are; we only know that one of them is near 4. Then we could call fzero like this:
>> fzero(@error_func, 4) ans = 3.0000
Success! We found one of the zeros.
The first argument is a function handle that names the M-file that evaluates the error function. The @ symbol allows us to name the function without calling it. The interesting thing here is that you are not actually calling error_func directly; you are just telling fzero where it is. In turn, fzero calls your error function—more than once, in fact.
The second argument is the initial guess. If we provide a different initial guess, we get a different root (at least sometimes).
>> fzero(@error_func, -2) ans = -1
Alternatively, if you know two values that bracket the root, you can provide both:
>> fzero(@error_func, [2,4]) ans = 3
The second argument here is actually a vector that contains two elements. The bracket operator is a convenient way (one of several) to create a new vector.
You might be curious to know how many times fzero calls your function, and where. If you modify error_func so that it displays the value of x every time it is called and then run fzero again, you get:
>> fzero(@error_func, [2,4]) x = 2 x = 4 x = 2.75000000000000 x = 3.03708133971292 x = 2.99755211623500 x = 2.99997750209270 x = 3.00000000025200 x = 3.00000000000000 x = 3 x = 3 ans = 3
Not surprisingly, it starts by computing f(2) and f(4). After each iteration, the interval that brackets the root gets smaller; fzero stops when the interval is so small that the estimated zero is correct to 16 digits. If you don’t need that much precision, you can tell fzero to give you a quicker, dirtier answer (see the documentation for details).
7.7 What could go wrong?
The most common problem people have with fzero is leaving out the @. In that case, you get something like:
>> fzero(error_func, [2,4])
Not enough input arguments.
Error in error_func (line 2)
res = x^2 - 2*x -3;
The error occurs as MATLAB treats the first argument as a function call, so it calls error_func with no arguments.
Another common problem is writing an error function that never assigns a value to the output variable. In general, functions should always assign a value to the output variable, but MATLAB doesn’t enforce this rule, so it is easy to forget. For example, if you write:
function res = error_func(x)
y = x^2 - 2*x -3
end
and then call it from the Command Window:
>> error_func(4) y = 5
It looks like it worked, but don’t be fooled. This function assigns a value to y, and it displays the result, but when the function ends, y disappears along with the function’s workspace. If you try to use it with fzero, you get
>> fzero(@error_func, [2,4]) y = -3 Error using fzero (line 231) FZERO cannot continue because user-supplied function_handle ==> error_func failed with the error below. Output argument "res" (and maybe others) not assigned during call to "error_func".
If you read it carefully, this is a pretty good error message (with the quibble that “output argument” is not a good synonym for “output variable”).
You would have seen the same error message when you called error_func from the interpreter, if only you had assigned the result to a variable:
>> x = error_func(4) y = 5 Output argument "res" (and maybe others) not assigned during call to "error_func".
You can avoid all of this if you remember these two rules:
- Functions should always assign values to their output variables.2
- When you call a function, you should always do something with the result (either assign it to a variable or use it as part of an expression, etc.).
When you write your own functions and use them yourself, it is easy for mistakes to go undetected. But when you use your functions with MATLAB functions like fzero, you have to get it right!
Yet another thing that can go wrong: if you provide an interval for the initial guess and it doesn’t actually contain a root, you get
>> fzero(@error_func, [0,1]) Error using fzero (line 272) The function values at the interval endpoints must differ in sign.
There is one other thing that can go wrong when you use fzero, but this one is less likely to be your fault. It is possible that fzero won’t be able to find a root.
fzero is generally pretty robust, so you may never have a problem, but you should remember that there is no guarantee that fzero will work, especially if you provide a single value as an initial guess. Even if you provide an interval that brackets a root, things can still go wrong if the error function is discontinuous.
7.8 Finding an initial guess
The better your initial guess (or interval) is, the more likely it is that fzero will work, and the fewer iterations it will need.
When you are solving problems in the real world, you will usually have some intuition about the answer. This intuition is often enough to provide a good initial guess for zero-finding.
Another approach is to plot the function and see if you can approximate the zeros visually. If you have a function, like error_func that takes a scalar input variable and returns a scalar output variable, you can plot it with ezplot:
>> ezplot(@error_func, [-2,5])
The first argument is a function handle; the second is the interval you want to plot the function in.
By default ezplot calls your function 100 times (each time with a different value of x, of course). So you probably want to make your function silent before you plot it.
7.9 More name collisions
Functions and variables occupy the same “name-space,” which means that whenever a name appears in an expression, MATLAB starts by looking for a variable with that name, and if there isn’t one, it looks for a function.
As a result, if you have a variable with the same name as a function, the variable shadows the function. For example, if you assign a value to sin, and then try to use the sin function, you might get an error:
>> sin = 3; >> x = 5; >> sin(x) Index exceeds matrix dimensions.
In this example, the problem is clear. Since the value of sin is a scalar, and a scalar is really a 1x1 matrix, MATLAB tries to access the 5th element of the matrix and finds that there isn’t one. Of course, if there were more distance between the assignment and the “function call,” this message would be pretty confusing.
But the only thing worse than getting an error message is not getting an error message. If the value of sin was a vector, or if the value of x was smaller, you would really be in trouble.
>> sin = 3; >> sin(1) ans = 3
Just to review, the sine of 1 is not 3!
The converse error can also happen if you try to access an undefined variable that also happens to be the name of a function. For example, if you have a function named f, and then try to increment a variable named f (and if you forget to initialize f), you get
>> f = f+1 Undefined function or variable 'f'.
At least, that’s what you get if you are lucky. If this happens inside a function, MATLAB tries to call f as a function, and you get this
>> f = f+1 Not enough input arguments. Error in f (line 3) y = x^2 - a
There is no universal way to avoid these kind of collisions, but you can improve your chances by choosing variable names that don’t shadow existing functions, and by choosing function names that you are unlikely to use as variables. That’s why, in Section 7.3, I called the error function error_func rather than f. I often give functions names that end in func, and that helps.
7.10 Debugging in four acts
When you are debugging a program, and especially if you are working on a hard bug, there are four things to try:
- reading:
- Examine your code, read it back to yourself, and check that it means what you meant to say.
- running:
- Experiment by making changes and running different versions. Often if you display the right thing at the right place in the program, the problem becomes obvious, but sometimes you have to spend some time to build scaffolding.
- ruminating:
- Take some time to think! What kind of error is it: syntax, run-time, logical? What information can you get from the error messages, or from the output of the program? What kind of error could cause the problem you’re seeing? What did you change last, before the problem appeared?
- retreating:
- At some point, the best thing to do is back off, undoing recent changes, until you get back to a program that works, and that you understand. Then you can starting rebuilding.
Beginning programmers sometimes get stuck on one of these activities and forget the others. Each activity comes with its own failure mode.
For example, reading your code might help if the problem is a typographical error, but not if the problem is a conceptual misunderstanding. If you don’t understand what your program does, you can read it 100 times and never see the error, because the error is in your head.
Running experiments can help, especially if you run small, simple tests. But if you run experiments without thinking or reading your code, you might fall into a pattern I call “random walk programming,” which is the process of making random changes until the program does the right thing. Needless to say, random walk programming can take a long time.
The way out is to take more time to think. Debugging is like an experimental science. You should have at least one hypothesis about what the problem is. If there are two or more possibilities, try to think of a test that would eliminate one of them.
Taking a break sometimes helps with the thinking. So does talking. If you explain the problem to someone else (or even yourself), you will sometimes find the answer before you finish asking the question.
But even the best debugging techniques will fail if there are too many errors, or if the code you are trying to fix is too big and complicated. Sometimes the best option is to retreat, simplifying the program until you get to something that works, and then rebuild.
Beginning programmers are often reluctant to retreat, because they can’t stand to delete a line of code (even if it’s wrong). If it makes you feel better, copy your program into another file before you start stripping it down. Then you can paste the pieces back in a little bit at a time.
To summarize, here’s the Ninth Theorem of Debugging:
Finding a hard bug requires reading, running, ruminating, and sometimes retreating. If you get stuck on one of these activities, try the others.
7.11 Glossary
- analytic solution:
- A way of solving an equation by performing algebraic operations and deriving an explicit way to compute a value that is only known implicitly.
- numerical solution:
- A way of solving an equation by finding a numerical value that satisfies the equation, often approximately.
- numerical method:
- A method (or algorithm) for generating a numerical solution.
- map:
- A correspondence between the elements of one set (the range) and the elements of another (the domain). You can think of sequences, vectors and functions as different kinds of maps.
- range:
- The set of values a map maps from.
- domain:
- The set of values a map maps to.
- discrete set:
- A set, like the integers, whose elements are countable.
- continuous set:
- A set, like the real numbers, whose elements are not countable. You can think of floating-point numbers as a continuous set.
- zero (of a function):
- A value in the range of a function that maps to 0.
- function handle:
- In MATLAB, a function handle is a way of referring to a function by name (and passing it as an argument) without calling it.
- shadow:
- A kind of name collision in which a new definition causes an existing definition to become invisible. In MATLAB, variable names can shadow built-in functions (with hilarious results).
7.12 Exercises
- Write a function called cheby6 that evaluates the
6th Chebyshev polynomial. It should take an input variable,
x, and return
32 x6 − 48 x4 + 18 x2 − 1 (4) - Use ezplot to display a graph of this function in the interval from 0 to 1. Estimate the location of any zeros in this range.
- Use fzero to find as many different roots as you can. Does fzero always find the root that is closest to the initial guess?
The density of a duck, ρ, is 0.3 g / cm3 (0.3 times the density of water).
The volume of a sphere with radius r is 4/3 π r3.
If a sphere with radius r is submerged in water to a depth d, the volume of the sphere below the water line is
| volume = |
| (3r d2 − d3) as long as d < 2 r (5) |
An object floats at the level where the weight of the displaced water equals the total weight of the object.
Assuming that a duck is a sphere with radius 10 cm, at what depth does a duck float?3
Here are some suggestions about how to proceed:
- Write an equation relating ρ, d, and r.
- Rearrange the equation so the right-hand side is zero. Our goal is to find values of d that are roots of this equation.
- Write a MATLAB function that evaluates this function. Test it, then make it a quiet function.
- Make a guess about the value of d0 to use as a starting place.
- Use fzero to find a root near d0.
- Check to make sure the result makes sense. In particular, check that d < 2 r, because otherwise the volume equation doesn’t work!
- Try different values of ρ and r and see if you get the effect you expect. What happens as ρ increases? Goes to infinity? Goes to zero? What happens as r increases? Goes to infinity? Goes to zero?
- 1
- To understand why this (sometimes) works, see https://en.wikipedia.org/wiki/Fixed-point_iteration.
- 2
- Well, ok, there are exceptions, including find_triples. Functions that don’t return a value are sometimes called “commands,” because they do something (like display values or generate a figure) but either don’t have an output variable or don’t make an assignment to it.
- 3
- This example is adapted from Gerald and Wheatley, Applied Numerical Analysis, Fourth Edition, Addison-Wesley, 1989.






