This HTML version of is provided for convenience, but it is not the best format for the book. In particular, some of the symbols are not rendered correctly.
You might prefer to read the PDF version, or you can buy a hardcopy here.
Chapter 2 Descriptive statistics
2.1 Means and averages
In the previous chapter, I mentioned three summary statistics—mean, variance and median—without explaining what they are. So before we go any farther, let’s take care of that.
If you have a sample of n values, xi, the mean, µ, is the sum of the values divided by the number of values; in other words
| µ = |
|
| xi |
The words “mean” and “average” are sometimes used interchangeably, but I will maintain this distinction:
- The “mean” of a sample is the summary statistic computed with the previous formula.
- An “average” is one of many summary statistics you might choose to describe the typical value or the central tendency of a sample.
Sometimes the mean is a good description of a set of values. For example, apples are all pretty much the same size (at least the ones sold in supermarkets). So if I buy 6 apples and the total weight is 3 pounds, it would be a reasonable summary to say they are about a half pound each.
But pumpkins are more diverse. Suppose I grow several varieties in my garden, and one day I harvest three decorative pumpkins that are 1 pound each, two pie pumpkins that are 3 pounds each, and one Atlantic Giant® pumpkin that weighs 591 pounds. The mean of this sample is 100 pounds, but if I told you “The average pumpkin in my garden is 100 pounds,” that would be wrong, or at least misleading.
In this example, there is no meaningful average because there is no typical pumpkin.
2.2 Variance
If there is no single number that summarizes pumpkin weights, we can do a little better with two numbers: mean and variance.
In the same way that the mean is intended to describe the central tendency, variance is intended to describe the spread. The variance of a set of values is
| σ2 = |
|
| (xi − µ)2 |
The term xi-µ is called the “deviation from the mean,” so variance is the mean squared deviation, which is why it is denoted σ2. The square root of variance, σ, is called the standard deviation.
By itself, variance is hard to interpret. One problem is that the units are strange; in this case the measurements are in pounds, so the variance is in pounds squared. Standard deviation is more meaningful; in this case the units are pounds.
Write a function called Pumpkin that uses functions from thinkstats.py to compute the mean, variance and standard deviation of the pumpkins weights in the previous section.
How big is the difference in the means compared to these standard deviations? What does this comparison suggest about the statistical significance of the difference?
If you have prior experience, you might have seen a formula for variance with n − 1 in the denominator, rather than n. This statistic is called the “sample variance,” and it is used to estimate the variance in a population using a sample. We will come back to this in Chapter 8.
2.3 Distributions
Summary statistics are concise, but dangerous, because they obscure the data. An alternative is to look at the distribution of the data, which describes how often each value appears.
The most common representation of a distribution is a histogram, which is a graph that shows the frequency or probability of each value.
In this context, frequency means the number of times a value appears in a dataset—it has nothing to do with the pitch of a sound or tuning of a radio signal. A probability is a frequency expressed as a fraction of the sample size, n.
In Python, an efficient way to compute frequencies is with a dictionary. Given a sequence of values, t:
hist = {}
for x in t:
hist[x] = hist.get(x, 0) + 1
The result is a dictionary that maps from values to frequencies. To get from frequencies to probabilities, we divide through by n, which is called normalization:
n = float(len(t))
pmf = {}
for x, freq in hist.items():
pmf[x] = freq / n
The normalized histogram is called a PMF, which stands for “probability mass function”; that is, it’s a function that maps from values to probabilities (I’ll explain “mass” in Section 6.3).
It might be confusing to call a Python dictionary a function. In mathematics, a function is a map from one set of values to another. In Python, we usually represent mathematical functions with function objects, but in this case we are using a dictionary (dictionaries are also called “maps,” if that helps).
2.4 Representing histograms
I wrote a Python module called Pmf.py that contains class definitions for Hist objects, which represent histograms, and Pmf objects, which represent PMFs. You can read the documentation at thinkstats.com/Pmf.html and download the code from thinkstats.com/Pmf.py.
The function MakeHistFromList takes a list of values and returns a new Hist object. You can test it in Python’s interactive mode:
>>> import Pmf >>> hist = Pmf.MakeHistFromList([1, 2, 2, 3, 5]) >>> print hist <Pmf.Hist object at 0xb76cf68c>
Pmf.Hist means that this object is a member of the Hist class, which is defined in the Pmf module. In general, I use upper case letters for the names of classes and functions, and lower case letters for variables.
Hist objects provide methods to look up values and their probabilities. Freq takes a value and returns its frequency:
>>> hist.Freq(2) 2
If you look up a value that has never appeared, the frequency is 0.
>>> hist.Freq(4) 0
Values returns an unsorted list of the values in the Hist:
>>> hist.Values() [1, 5, 3, 2]
To loop through the values in order, you can use the built-in function sorted:
for val in sorted(hist.Values()):
print val, hist.Freq(val)
If you are planning to look up all of the frequencies, it is more efficient to use Items, which returns an unsorted list of value-frequency pairs:
for val, freq in hist.Items():
print val, freq
As a more challenging version, write a function called AllModes that takes a Hist object and returns a list of value-frequency pairs in descending order of frequency. Hint: the operator module provides a function called itemgetter which you can pass as a key to sorted.
2.5 Plotting histograms
There are a number of Python packages for making figures and graphs. The one I will demonstrate is pyplot, which is part of the matplotlib package at http://matplotlib.sourceforge.net.
This package is included in many Python installations. To see whether you have it, launch the Python interpreter and run:
import matplotlib.pyplot as pyplot pyplot.pie([1,2,3]) pyplot.show()
If you have matplotlib you should see a simple pie chart; otherwise you will have to install it.
Histograms and PMFs are most often plotted as bar charts. The pyplot function to draw a bar chart is bar. Hist objects provide a method called Render that returns a sorted list of values and a list of the corresponding frequencies, which is the format bar expects:
>>> vals, freqs = hist.Render() >>> rectangles = pyplot.bar(vals, freqs) >>> pyplot.show()
I wrote a module called myplot.py that provides functions for plotting histograms, PMFs and other objects we will see soon. You can read the documentation at thinkstats.com/myplot.html and download the code from thinkstats.com/myplot.py. Or you can use pyplot directly, if you prefer. Either way, you can find the documentation for pyplot on the web.
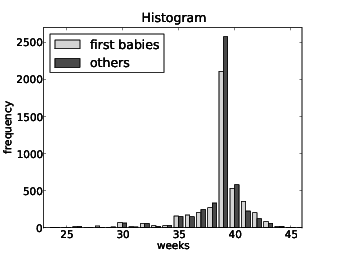
Figure 2.1 shows histograms of pregnancy lengths for first babies and others.
Figure 2.1: Histogram of pregnancy lengths.
Histograms are useful because they make the following features immediately apparent:
- Mode:
- The most common value in a distribution is called the mode. In Figure 2.1 there is a clear mode at 39 weeks. In this case, the mode is the summary statistic that does the best job of describing the typical value.
- Shape:
- Around the mode, the distribution is asymmetric; it drops off quickly to the right and more slowly to the left. From a medical point of view, this makes sense. Babies are often born early, but seldom later than 42 weeks. Also, the right side of the distribution is truncated because doctors often intervene after 42 weeks.
- Outliers:
- Values far from the mode are called outliers. Some of these are just unusual cases, like babies born at 30 weeks. But many of them are probably due to errors, either in the reporting or recording of data.
Although histograms make some features apparent, they are usually not useful for comparing two distributions. In this example, there are fewer “first babies” than “others,” so some of the apparent differences in the histograms are due to sample sizes. We can address this problem using PMFs.
2.6 Representing PMFs
Pmf.py provides a class called Pmf that represents PMFs. The notation can be confusing, but here it is: Pmf is the name of the module and also the class, so the full name of the class is Pmf.Pmf. I often use pmf as a variable name. Finally, in the text, I use PMF to refer to the general concept of a probability mass function, independent of my implementation.
To create a Pmf object, use MakePmfFromList, which takes a list of values:
>>> import Pmf >>> pmf = Pmf.MakePmfFromList([1, 2, 2, 3, 5]) >>> print pmf <Pmf.Pmf object at 0xb76cf68c>
Pmf and Hist objects are similar in many ways. The methods Values and Items work the same way for both types. The biggest difference is that a Hist maps from values to integer counters; a Pmf maps from values to floating-point probabilities.
To look up the probability associated with a value, use Prob:
>>> pmf.Prob(2) 0.4
You can modify an existing Pmf by incrementing the probability associated with a value:
>>> pmf.Incr(2, 0.2) >>> pmf.Prob(2) 0.6
Or you can multiply a probability by a factor:
>>> pmf.Mult(2, 0.5) >>> pmf.Prob(2) 0.3
If you modify a Pmf, the result may not be normalized; that is, the probabilities may no longer add up to 1. To check, you can call Total, which returns the sum of the probabilities:
>>> pmf.Total() 0.9
To renormalize, call Normalize:
>>> pmf.Normalize() >>> pmf.Total() 1.0
Pmf objects provide a Copy method so you can make and modify a copy without affecting the original.
As part of survival analysis, it is often useful to compute the remaining lifetime of, for example, a mechanical component. If we know the distribution of lifetimes and the age of the component, we can compute the distribution of remaining lifetimes.
Write a function called RemainingLifetime that takes a Pmf of lifetimes and an age, and returns a new Pmf that represents the distribution of remaining lifetimes.
| µ = |
| pi xi |
| σ2 = |
| pi (xi − µ)2 |
2.7 Plotting PMFs
There are two common ways to plot Pmfs:
- To plot a Pmf as a bar graph, you can use pyplot.bar or myplot.Hist. Bar graphs are most useful if the number of values in the Pmf is small.
- To plot a Pmf as a line, you can use pyplot.plot or myplot.Pmf. Line plots are most useful if there are a large number of values and the Pmf is smooth.
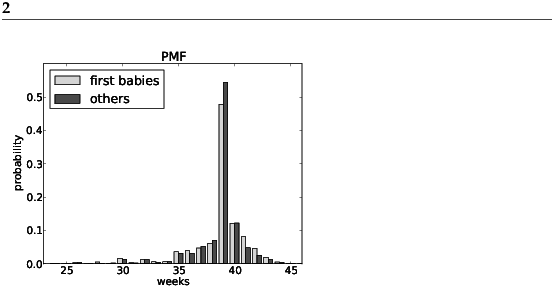
Figure 2.2: PMF of pregnancy lengths.
Figure 2.2 shows the PMF of pregnancy lengths as a bar graph. Using the PMF, we can see more clearly where the distributions differ. First babies seem to be less likely to arrive on time (week 39) and more likely to be a late (weeks 41 and 42).
The code that generates the figures in this chapters is available from http://thinkstats.com/descriptive.py. To run it, you will need the modules it imports and the data from the NSFG (see Section 1.3).
Note: pyplot provides a function called hist that takes a sequence of values, computes the histogram and plots it. Since I use Hist objects, I usually don’t use pyplot.hist.
2.8 Outliers
Outliers are values that are far from the central tendency. Outliers might be caused by errors in collecting or processing the data, or they might be correct but unusual measurements. It is always a good idea to check for outliers, and sometimes it is useful and appropriate to discard them.
In the list of pregnancy lengths for live births, the 10 lowest values are {0, 4, 9, 13, 17, 17, 18, 19, 20, 21}. Values below 20 weeks are certainly errors, and values higher than 30 weeks are probably legitimate. But values in between are hard to interpret.
On the other end, the highest values are:
weeks count 43 148 44 46 45 10 46 1 47 1 48 7 50 2
Again, some values are almost certainly errors, but it is hard to know for sure. One option is to trim the data by discarding some fraction of the highest and lowest values (see http://wikipedia.org/wiki/Truncated_mean).
2.9 Other visualizations
Histograms and PMFs are useful for exploratory data analysis; once you have an idea what is going on, it is often useful to design a visualization that focuses on the apparent effect.
In the NSFG data, the biggest differences in the distributions are near the mode. So it makes sense to zoom in on that part of the graph, and to transform the data to emphasize differences.
Figure 2.3 shows the difference between the PMFs for weeks 35–45. I multiplied by 100 to express the differences in percentage points.
Figure 2.3: Difference in percentage, by week.
This figure makes the pattern clearer: first babies are less likely to be born in week 39, and somewhat more likely to be born in weeks 41 and 42.
2.10 Relative risk
We started with the question, “Do first babies arrive late?” To make that more precise, let’s say that a baby is early if it is born during Week 37 or earlier, on time if it is born during Week 38, 39 or 40, and late if it is born during Week 41 or later. Ranges like these that are used to group data are called bins.
Make three PMFs, one for first babies, one for others, and one for all live births. For each PMF, compute the probability of being born early, on time, or late.
One way to summarize data like this is with relative risk, which is a ratio of two probabilities. For example, the probability that a first baby is born early is 18.2%. For other babies it is 16.8%, so the relative risk is 1.08. That means that first babies are about 8% more likely to be early.
Write code to confirm that result, then compute the relative risks of being born on time and being late. You can download a solution from http://thinkstats.com/risk.py.
2.11 Conditional probability
Imagine that someone you know is pregnant, and it is the beginning of Week 39. What is the chance that the baby will be born in the next week? How much does the answer change if it’s a first baby?
We can answer these questions by computing a conditional probability, which is (ahem!) a probability that depends on a condition. In this case, the condition is that we know the baby didn’t arrive during Weeks 0–38.
Here’s one way to do it:
- Given a PMF, generate a fake cohort of 1000 pregnancies. For each number of weeks, x, the number of pregnancies with duration x is 1000 PMF(x).
- Remove from the cohort all pregnancies with length less than 39.
- Compute the PMF of the remaining durations; the result is the conditional PMF.
- Evaluate the conditional PMF at x = 39 weeks.
This algorithm is conceptually clear, but not very efficient. A simple alternative is to remove from the distribution the values less than 39 and then renormalize.
Generalize the function to compute the probability that a baby will be born during Week x, given that it was not born prior to Week x, for all x. Plot this value as a function of x for first babies and others.
You can download a solution to this problem from http://thinkstats.com/conditional.py.
2.12 Reporting results
At this point we have explored the data and seen several apparent effects. For now, let’s assume that these effects are real (but let’s remember that it’s an assumption). How should we report these results?
The answer might depend on who is asking the question. For example, a scientist might be interested in any (real) effect, no matter how small. A doctor might only care about effects that are clinically significant; that is, differences that affect treatment decisions. A pregnant woman might be interested in results that are relevant to her, like the conditional probabilities in the previous section.
How you report results also depends on your goals. If you are trying to demonstrate the significance of an effect, you might choose summary statistics, like relative risk, that emphasize differences. If you are trying to reassure a patient, you might choose statistics that put the differences in context.
Which summary statistics would you use if you wanted to get a story on the evening news? Which ones would you use if you wanted to reassure an anxious patient?
Finally, imagine that you are Cecil Adams, author of The Straight Dope (http://straightdope.com), and your job is to answer the question, “Do first babies arrive late?” Write a paragraph that uses the results in this chapter to answer the question clearly, precisely, and accurately.
2.13 Glossary
- central tendency:
- A characteristic of a sample or population; intuitively, it is the most average value.
- spread:
- A characteristic of a sample or population; intuitively, it describes how much variability there is.
- variance:
- A summary statistic often used to quantify spread.
- standard deviation:
- The square root of variance, also used as a measure of spread.
- frequency:
- The number of times a value appears in a sample.
- histogram:
- A mapping from values to frequencies, or a graph that shows this mapping.
- probability:
- A frequency expressed as a fraction of the sample size.
- normalization:
- The process of dividing a frequency by a sample size to get a probability.
- distribution:
- A summary of the values that appear in a sample and the frequency, or probability, of each.
- PMF:
- Probability mass function: a representation of a distribution as a function that maps from values to probabilities.
- mode:
- The most frequent value in a sample.
- outlier:
- A value far from the central tendency.
- trim:
- To remove outliers from a dataset.
- bin:
- A range used to group nearby values.
- relative risk:
- A ratio of two probabilities, often used to measure a difference between distributions.
- conditional probability:
- A probability computed under the assumption that some condition holds.
- clinically significant:
- A result, like a difference between groups, that is relevant in practice.
Like this book?
Are you using one of our books in a class?
We'd like to know about it. Please consider filling out this short survey.